K-means的缺点
K-means要求必须预设k值 - 需要事先知道或估计簇的数量,且其出初始点十分敏感,不同的初始中心可能导致不同结果,且其直接假设簇是球形的,这在一定程度上是不可能的,而层次聚类(hierarchical clustering)则没有这种问题,他在使用前不需要提前限定簇的个数,且也不强求分类之后的簇必须是球形的,这给层次聚类带来了巨大的应用前景,层次聚类在实际问题的解决上分为两种算法:
凝聚的层次聚类: AGNES算法(AGglomerative NESting) ==> 采用自底向上的策略。 最初将每个对象作为一个簇,然后这些簇根据某些准则被一步步合并,两个簇间的距离可以由这两个不同簇中距离最近的数据点的相似度来确定;聚类的合并过程反复进行直到所有的对象满足簇数目。
分裂的层次聚类: DIANA算法(DIvisive ANAlysis) ==> 采用自顶向下的策略。 首先将所有对象置于一个簇中,然后按照某种既定的规则逐渐细分为越来越小的簇(比如最大的欧式距离),直到达到某个终结条件(簇数目或者簇距离达到阈值)。
相较而言,AGNES算法在使用中有着更广泛的应用前景,且其也已经研究较为透彻。
AGNES算法的原理
在AGNES中,由于簇的生成不是事先预定的,因此我们需要考虑距离采取的是哪一种度量方法,一般来说有三种距离统计方法:
最小连接距离法(Single Linkage)
其表示如下,在度量距离时,我们采取的是不同簇之间的最短距离:d(R, S) = \min_{x_R \in R, x_S \in S} d(x_R, x_S)
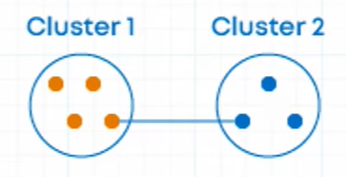
2.最大连接距离法(Complete Linkage)
取两个簇中距离最远的两个点的距离作为这两个簇的距离。 其表示的关系如下图所示,计算公式为:d(R, S) = \max_{x_R \in R, x_S \in S} d(x_R, x_S)
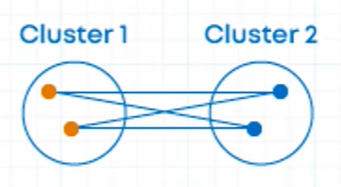
3.平均关联 (Average-Linkage)
这种方法是AGNES算法常用的距离计算方法,其方法是将两个簇之间的所有点的距离两两算在一起,全部求平均值,这种方法是最为可靠的,其计算的公式如下:d(R, S) = \frac{1}{|R||S|} \sum_{x_R \in R, x_S \in S} d(x_R, x_S)
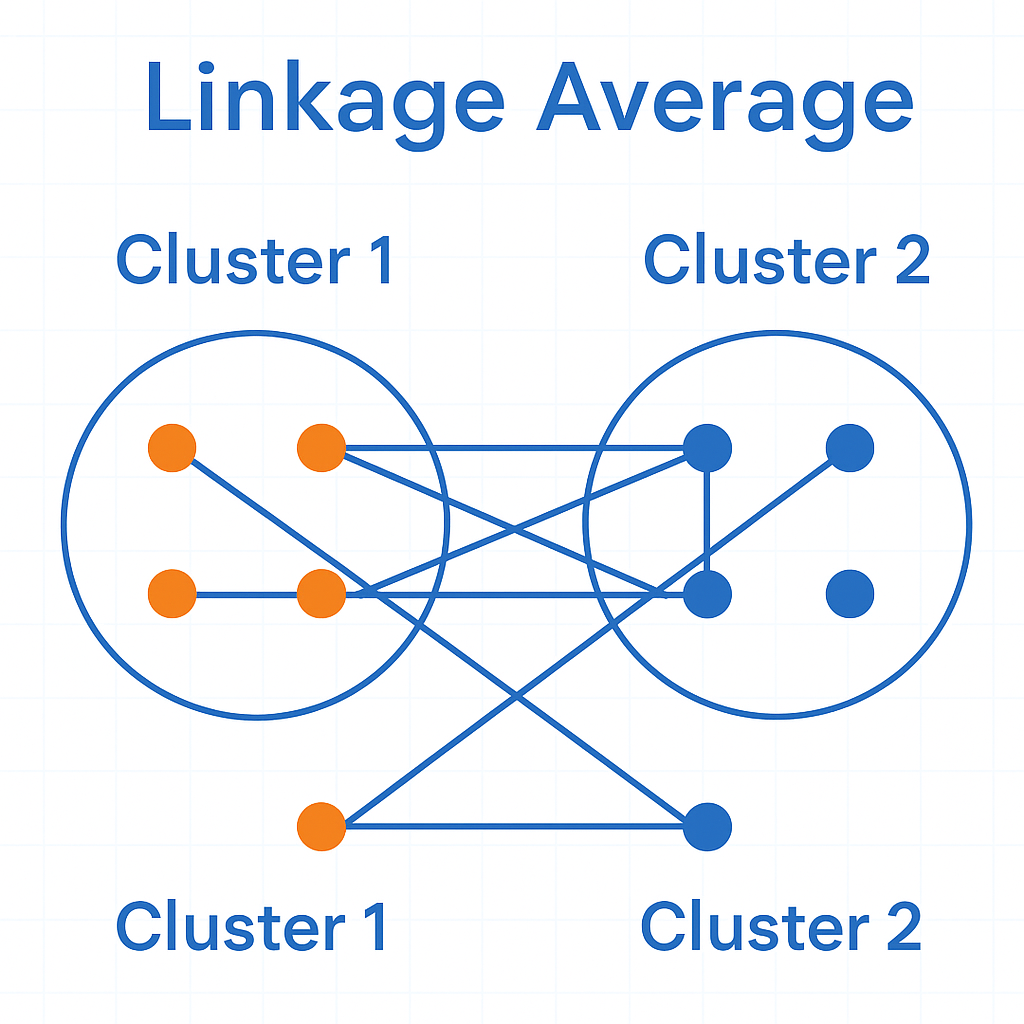
AGNES的算法流程如下:
初始化,将每个样本都视为一个簇
计算各个簇之间的距离
寻找最近的两个簇,并将他们合并为一类
重复步骤(2)和步骤(3),知道所有样本归为一类。
AGNES的实例分析
某农业研究所收集了30个西瓜样本的数据,包括每个西瓜的密度和含糖量两个特征。现在需要利用AGNES(层次聚类)算法对这些西瓜进行分类,以帮助农民识别不同品质的西瓜。
实验的数据集如下:
| 编号 | 密度 (g/cm³) | 含糖量 |
|---|---|---|
| 1 | 0.697 | 0.460 |
| 2 | 0.774 | 0.376 |
| 3 | 0.634 | 0.264 |
| 4 | 0.608 | 0.318 |
| 5 | 0.556 | 0.215 |
| 6 | 0.403 | 0.237 |
| 7 | 0.481 | 0.149 |
| 8 | 0.437 | 0.211 |
| 9 | 0.666 | 0.091 |
| 10 | 0.243 | 0.267 |
| 11 | 0.245 | 0.057 |
| 12 | 0.343 | 0.099 |
| 13 | 0.639 | 0.161 |
| 14 | 0.657 | 0.198 |
| 15 | 0.360 | 0.370 |
| 16 | 0.593 | 0.042 |
| 17 | 0.719 | 0.103 |
| 18 | 0.359 | 0.188 |
| 19 | 0.339 | 0.241 |
| 20 | 0.282 | 0.257 |
| 21 | 0.748 | 0.232 |
| 22 | 0.714 | 0.346 |
| 23 | 0.483 | 0.312 |
| 24 | 0.478 | 0.437 |
| 25 | 0.525 | 0.369 |
| 26 | 0.751 | 0.489 |
| 27 | 0.532 | 0.472 |
| 28 | 0.473 | 0.376 |
| 29 | 0.725 | 0.445 |
| 30 | 0.446 | 0.459 |
处理的python代码如下:
import math
import matplotlib.pyplot as plt
import numpy as np
def dist(node1, node2):
"""
计算欧几里得距离,node1,node2分别为两个元组
:param node1: 第一个数据点
:param node2: 第二个数据点
:return: 欧几里得距离
"""
return math.sqrt(math.pow(node1[0]-node2[0], 2) + math.pow(node1[1]-node2[1], 2))
def dist_min(cluster_x, cluster_y):
"""
Single Linkage (最小距离)
又叫做 nearest-neighbor,就是取两个类中距离最近的两个样本的距离作为这两个集合的距离。
:param cluster_x: 簇类x
:param cluster_y: 簇类y
:return: 最小距离
"""
return min(dist(node1, node2) for node1 in cluster_x for node2 in cluster_y)
def dist_max(cluster_x, cluster_y):
"""
Complete Linkage (最大距离)
这个则完全是 Single Linkage 的反面极端,取两个集合中距离最远的两个点的距离作为两个集合的距离。
:param cluster_x: 簇类x
:param cluster_y: 簇类y
:return: 最大距离
"""
return max(dist(node1, node2) for node1 in cluster_x for node2 in cluster_y)
def dist_avg(cluster_x, cluster_y):
"""
Average Linkage (平均距离)
这种方法就是把两个集合中的点两两的距离全部放在一起求均值,相对也能得到合适一点的结果。
:param cluster_x: 簇类x
:param cluster_y: 簇类y
:return: 平均距离
"""
return sum(dist(node1, node2) for node1 in cluster_x for node2 in cluster_y) / (len(cluster_x) * len(cluster_y))
def find_min(distance_matrix):
"""
找出距离最近的两个簇下标
:param distance_matrix: 距离矩阵
:return: (x索引, y索引, 最小距离)
"""
min_dist = float('inf')
x = 0
y = 0
for i in range(len(distance_matrix)):
for j in range(len(distance_matrix[i])):
if i != j and distance_matrix[i][j] < min_dist:
min_dist = distance_matrix[i][j]
x = i
y = j
return (x, y, min_dist)
def AGNES(dataset, distance_method, k):
"""
AGNES聚类算法模型
:param dataset: 数据集
:param distance_method: 计算簇类距离的方法
:param k: 目标簇类数目
:return: 聚类结果
"""
print(f"数据集大小: {len(dataset)}")
# 初始化簇类集合 - 每个样本作为一个簇
cluster_set = []
for node in dataset:
cluster_set.append([node])
print('初始簇类集合:')
print(f"共有 {len(cluster_set)} 个簇")
# 计算初始距离矩阵
distance_matrix = []
for cluster_x in cluster_set:
distance_list = []
for cluster_y in cluster_set:
if cluster_x == cluster_y:
distance_list.append(0)
else:
distance_list.append(distance_method(cluster_x, cluster_y))
distance_matrix.append(distance_list)
print(f'初始距离矩阵维度: {len(distance_matrix)} x {len(distance_matrix[0])}')
q = len(dataset)
iteration = 0
# 合并更新
while q > k:
iteration += 1
print(f"第 {iteration} 次迭代,当前簇数: {q}")
# 找到距离最近的两个簇
id_x, id_y, min_distance = find_min(distance_matrix)
print(f"合并簇 {id_x} 和簇 {id_y},距离: {min_distance:.4f}")
# 合并簇(确保id_x < id_y,先删除索引大的)
if id_x > id_y:
id_x, id_y = id_y, id_x
cluster_set[id_x].extend(cluster_set[id_y])
del cluster_set[id_y] # 删除已合并的簇
# 重新计算距离矩阵
distance_matrix = []
for cluster_x in cluster_set:
distance_list = []
for cluster_y in cluster_set:
if cluster_x == cluster_y:
distance_list.append(0)
else:
distance_list.append(distance_method(cluster_x, cluster_y))
distance_matrix.append(distance_list)
q -= 1
print(f"聚类完成!最终得到 {len(cluster_set)} 个簇")
return cluster_set
def draw(cluster_set):
"""
绘制聚类结果
:param cluster_set: 聚类结果
:return: None
"""
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
color_list = ['red', 'blue', 'green', 'orange', 'purple', 'brown', 'pink', 'gray', 'olive', 'cyan']
marker_list = ['o', 's', '^', 'D', 'v', '<', '>', 'p', '*', 'h']
plt.figure(figsize=(10, 8))
for cluster_idx, cluster in enumerate(cluster_set):
coo_x = [] # x坐标列表(密度)
coo_y = [] # y坐标列表(含糖量)
for node in cluster:
coo_x.append(node[0])
coo_y.append(node[1])
plt.scatter(coo_x, coo_y,
marker=marker_list[cluster_idx % len(marker_list)],
color=color_list[cluster_idx % len(color_list)],
label=f'簇 {cluster_idx + 1} ({len(cluster)}个样本)',
s=100, alpha=0.7)
plt.xlabel('密度')
plt.ylabel('含糖量')
plt.title('AGNES聚类结果 - 西瓜数据集')
plt.legend(loc='upper right')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
def print_cluster_details(cluster_set):
"""
打印聚类详细信息
:param cluster_set: 聚类结果
"""
print("\n聚类详细结果:")
print("=" * 50)
for i, cluster in enumerate(cluster_set):
print(f"簇 {i+1}: 包含 {len(cluster)} 个样本")
for j, point in enumerate(cluster):
print(f" 样本 {j+1}: 密度={point[0]:.3f}, 含糖量={point[1]:.3f}")
# 计算簇中心
center_x = sum(point[0] for point in cluster) / len(cluster)
center_y = sum(point[1] for point in cluster) / len(cluster)
print(f" 簇中心: 密度={center_x:.3f}, 含糖量={center_y:.3f}")
print()
if __name__ == "__main__":
# 数据集:每三个是一组分别是西瓜的编号,密度,含糖量
data = """
1,0.697,0.46,2,0.774,0.376,3,0.634,0.264,4,0.608,0.318,5,0.556,0.215,
6,0.403,0.237,7,0.481,0.149,8,0.437,0.211,9,0.666,0.091,10,0.243,0.267,
11,0.245,0.057,12,0.343,0.099,13,0.639,0.161,14,0.657,0.198,15,0.36,0.37,
16,0.593,0.042,17,0.719,0.103,18,0.359,0.188,19,0.339,0.241,20,0.282,0.257,
21,0.748,0.232,22,0.714,0.346,23,0.483,0.312,24,0.478,0.437,25,0.525,0.369,
26,0.751,0.489,27,0.532,0.472,28,0.473,0.376,29,0.725,0.445,30,0.446,0.459"""
# 数据处理 dataset是30个样本(密度,含糖量)的列表
a = data.split(',')
dataset = [(float(a[i]), float(a[i+1])) for i in range(1, len(a)-1, 3)]
print("开始AGNES聚类算法")
print("=" * 30)
# 执行聚类(聚成3类)
cluster_set = AGNES(dataset, dist_avg, 3)
print('\n最终聚类结果:')
print(cluster_set)
# 打印详细信息
print_cluster_details(cluster_set)
# 绘制结果
draw(cluster_set)
print("聚类完成!")最终的聚类结果如下的表格所示:
聚类结果
最终聚类结果
- 簇1: [(0.697, 0.46), (0.725, 0.445), (0.751, 0.489), (0.774, 0.376), (0.714, 0.346)]
- 簇2: [(0.634, 0.264), (0.608, 0.318), (0.556, 0.215), (0.481, 0.149), (0.666, 0.091), (0.719, 0.103), (0.639, 0.161), (0.657, 0.198), (0.748, 0.232), (0.593, 0.042)]
- 簇3: [(0.403, 0.237), (0.437, 0.211), (0.359, 0.188), (0.339, 0.241), (0.243, 0.267), (0.282, 0.257), (0.245, 0.057), (0.343, 0.099), (0.36, 0.37), (0.483, 0.312), (0.525, 0.369), (0.473, 0.376), (0.478, 0.437), (0.446, 0.459), (0.532, 0.472)]
聚类详细结果
簇 1: 包含 5 个样本(优质西瓜)
| 样本 | 密度 | 含糖量 |
|---|---|---|
| 1 | 0.697 | 0.460 |
| 2 | 0.725 | 0.445 |
| 3 | 0.751 | 0.489 |
| 4 | 0.774 | 0.376 |
| 5 | 0.714 | 0.346 |
簇中心: 密度=0.732, 含糖量=0.423
簇 2: 包含 10 个样本(中等西瓜)
| 样本 | 密度 | 含糖量 |
|---|---|---|
| 1 | 0.634 | 0.264 |
| 2 | 0.608 | 0.318 |
| 3 | 0.556 | 0.215 |
| 4 | 0.481 | 0.149 |
| 5 | 0.666 | 0.091 |
| 6 | 0.719 | 0.103 |
| 7 | 0.639 | 0.161 |
| 8 | 0.657 | 0.198 |
| 9 | 0.748 | 0.232 |
| 10 | 0.593 | 0.042 |
簇中心: 密度=0.630, 含糖量=0.177
簇 3: 包含 15 个样本(普通西瓜)
| 样本 | 密度 | 含糖量 |
|---|---|---|
| 1 | 0.403 | 0.237 |
| 2 | 0.437 | 0.211 |
| 3 | 0.359 | 0.188 |
| 4 | 0.339 | 0.241 |
| 5 | 0.243 | 0.267 |
| 6 | 0.282 | 0.257 |
| 7 | 0.245 | 0.057 |
| 8 | 0.343 | 0.099 |
| 9 | 0.360 | 0.370 |
| 10 | 0.483 | 0.312 |
| 11 | 0.525 | 0.369 |
| 12 | 0.473 | 0.376 |
| 13 | 0.478 | 0.437 |
| 14 | 0.446 | 0.459 |
| 15 | 0.532 | 0.472 |
簇中心: 密度=0.397, 含糖量=0.290
聚类结果分析
簇特征对比
| 簇编号 | 样本数量 | 密度范围 | 含糖量范围 | 西瓜品质 |
|---|---|---|---|---|
| 簇 1 | 5个 | 0.697-0.774 | 0.346-0.489 | 优质西瓜 |
| 簇 2 | 10个 | 0.481-0.748 | 0.042-0.318 | 中等西瓜 |
| 簇 3 | 15个 | 0.243-0.532 | 0.057-0.472 | 普通西瓜 |
实验结论
- 簇1(优质西瓜): 密度和含糖量都较高,可能是最优质的西瓜
- 簇2(中等西瓜): 密度中等但含糖量偏低,品质一般
- 簇3(普通西瓜): 样本数量最多,密度较低但含糖量分布较广,品质参差不齐
- AGNES算法成功将30个西瓜样本分为3个具有明显特征差异的簇
- 聚类结果符合实际认知:高密度高含糖量的西瓜品质最好


