传统K-means
聚类分析是机器学习与数据挖掘中的一项重要任务,旨在将相似的数据对象划分为同一组(簇),同时确保不同组之间的差异性。在众多聚类算法中,K-means因其简洁性、高效性和可扩展性而成为最广泛使用的算法之一。K-means的核心思想是通过迭代优化,将数据划分为K个簇,使得每个数据点归属于离其最近的簇中心(质心),同时最小化簇内平方误差(SSE)。
K-means的具体步骤:
首先根据matlab绘制不同K值(聚类的类数条件下)的WCSS(聚类内误差平方和)图像。随后根据图像的肘部原则确定K的值。
我们假设有如下的几组数据,以蓝色散点图表示个体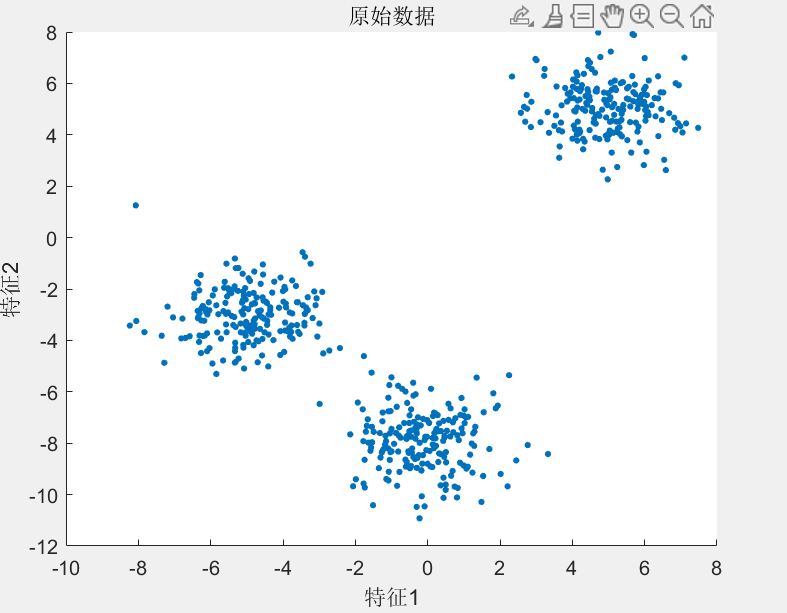
在如下图中我们发现箭头处是凸出的最后位置,成为肘部,其对应着K=3.因此我们应当将其分为3类。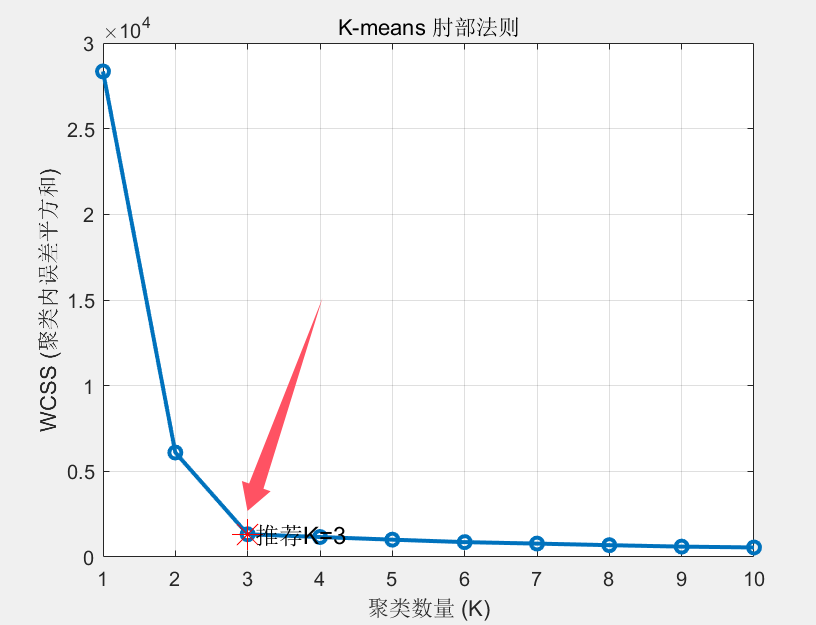
从数据集中随机选择K个数据点作为操作质心。(随机选择质心正是K-means的缺陷所在)
对数据集中的其他点,计算其与每一个质心之间的距离,离哪个质心近,就划分到对应的集合
常见的距离判断如下(在matlab中若不特别指明,一般都是指欧式距离)
再计算各质心集的均值向量,最后重新划分集合。
迭代循环,得到最终聚类结果。重复第三步和第四步,直到满足迭代终止条件
终止条件的设定:
1.人为确定迭代的次数。例如:预先设定迭代210次
2.类中心点不再发生变化或没有对象被分配给新的类
3.根据簇C_1,C_2...C_k则当满足最小化误差E时,停止迭代:(使用启发式算法解决)
式中u_i是簇质心的均值向量。E = \sum_{i=1}^k \sum_{x \in C_i} |x - u_i|^2
最后我们得到如下的结果图:
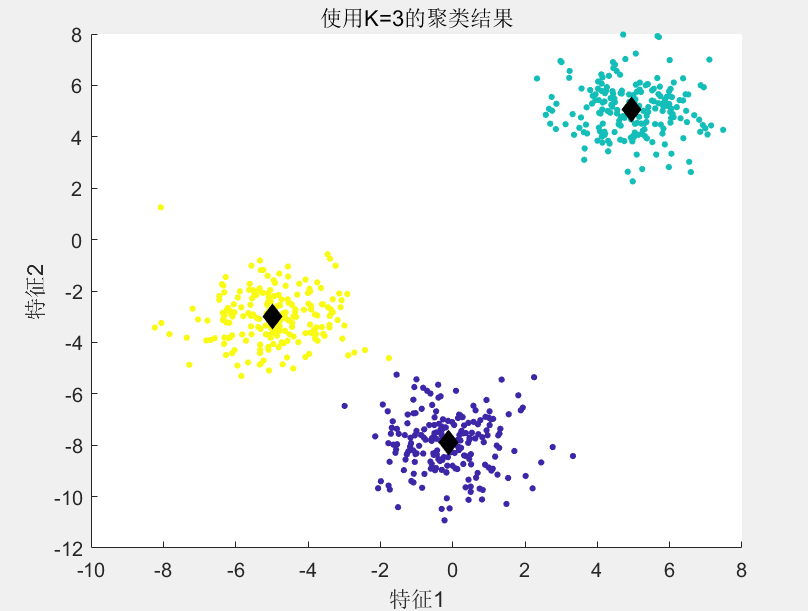
抽象指标的K-means距离问题(Jaccobd距离)
抽象指标指的是像性别、是否发烧这样难以直接度量的属性。而我们所需要做的就是把这些抽象指标划为可以度量的数值。这让我们想到了运筹学中的0-1变量方法。倘若我们利用1表示"有",0表示“无”。那么我们便解决了量化的问题。
Jaccobd距离的使用可以参考如下表格。
| 指标一 | 指标二 | |
|---|---|---|
| A | 有 | 有 |
| B | 无 | 无 |
我们定义1表示有,0表示无,那么即可得到下图:
| 指标一 | 指标二 | |
|---|---|---|
| A | 1 | 1 |
| B | 0 | 0 |
再考虑更多的指标,同样使用这种量化方式,我们可以得到下表:
| A \ B | 1 | 0 | sum |
|---|---|---|---|
| 1 | a | b | a + b |
| 0 | c | d | c + d |
| sum | a+c | b+d | T |
式中T=a+b+c+d
最终我们仿照jaccobd距离的定义得到了其表达式:
式中b和c反应的是A与B相异的成分。那么很明显:Jaccobd距离越小,二者越相似,越有可能被聚在同一类。
传统k-means的实现代码
% 清空工作区并关闭所有图像
clear all;
close all;
clc;
% 生成示例数据(或加载自己的数据)
% 这里生成3个明显聚类的二维数据作为示例
rng(42); % 设置随机种子确保可重复性
n = 200;
cluster1 = randn(n, 2) + repmat([5 5], n, 1);
cluster2 = randn(n, 2) + repmat([-5 -3], n, 1);
cluster3 = randn(n, 2) + repmat([0 -8], n, 1);
data = [cluster1; cluster2; cluster3];
% 可视化原始数据
figure;
scatter(data(:,1), data(:,2), 10, 'filled');
title('原始数据');
xlabel('特征1'); ylabel('特征2');
% 通过肘部原则确定最佳K值
maxK = 10; % 最大尝试的聚类数
wcss = zeros(maxK, 1); % 存储每个K值对应的WCSS
for k = 1:maxK
% 运行K-means
[idx, centers] = kmeans(data, k, 'Distance', 'sqeuclidean', 'Replicates', 10);
% 计算WCSS (Within-Cluster Sum of Squares)
wcssk = 0;
for i = 1:k
cluster_points = data(idx == i, :);
center = centers(i, :);
wcssk = wcssk + sum(sum((cluster_points - center).^2, 2));
end
wcss(k) = wcssk;
end
% 绘制肘部图
figure;
plot(1:maxK, wcss, '-o', 'LineWidth', 2);
title('K-means 肘部法则');
xlabel('聚类数量 (K)');
ylabel('WCSS (聚类内误差平方和)');
grid on;
% 可选:使用自动方法找到肘部点
diff_wcss = diff(wcss);
% 计算曲线斜率变化
change_rate = diff(diff_wcss) ./ diff_wcss(1:end-1);
[~, elbow_idx] = min(change_rate);
elbow_k = elbow_idx + 1;
% 在图上标记肘部点
hold on;
plot(elbow_k, wcss(elbow_k), 'r*', 'MarkerSize', 15);
text(elbow_k + 0.1, wcss(elbow_k), ['推荐K=' num2str(elbow_k)], 'FontSize', 12);
hold off;
% 使用推荐的K值可视化聚类结果
[idx_optimal, centers_optimal] = kmeans(data, elbow_k, 'Distance', 'sqeuclidean', 'Replicates', 10);
% 可视化最终聚类结果
figure;
scatter(data(:,1), data(:,2), 10, idx_optimal, 'filled');
hold on;
scatter(centers_optimal(:,1), centers_optimal(:,2), 100, 'k', 'filled', 'diamond');
title(['使用K=' num2str(elbow_k) '的聚类结果']);
xlabel('特征1'); ylabel('特征2');K-means++
传统K-means++的缺陷在于聚类中心的随机选取,这会导致出现较大的误差。因此算法常陷入局部最优。
K-means++算法中对于聚类中心的动态选取
随机选择一个样本点作为第一个聚类中心
计算剩下的每一个样本点距离已选聚类中心的最小距离D(x_i)每次迭代后可得到\sum D(x_i)
针对每一个样本点,可以计算每个样本点被选为下一个聚类中心的概率或权重
P = \frac{D(x_i)}{\sum D(x_i)^2},
选择P最大的样本作为下一个聚类中心。重复第2、第3步,直到选够k个聚类中心,迭代结束
选取的是最小距离D(x_i) 中的最大值,而不是最大值的最大值,是为了更容易选到同一类别中的样本点
可以使初始聚类中心更加分散,使结果更加理想。
K-means++仅做了聚类中心选取的优化,但是可以使聚类的效果更加显著。其余走K-means即可。
K-means++运行的结果如图:
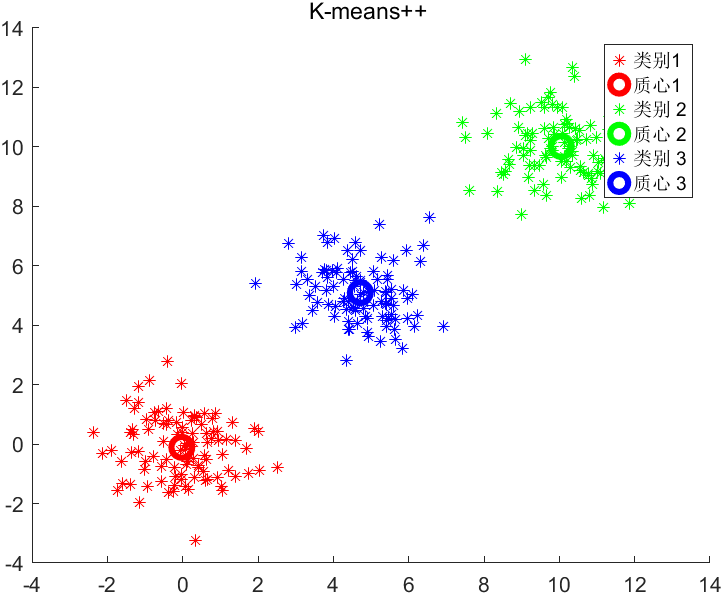
K-means matlab代码实现
代码来源:K-means++聚类算法(matlab实现)_k中心点聚类算法 matlab-CSDN博客
% 生成数据
X = [randn(100,2); randn(100,2)+5; randn(100,2)+10];
%聚类种类
K = 3;
max_iters = 10;
centroids = init_centroids(X, K);
% 迭代更新簇分配和簇质心
for i = 1:max_iters
% 簇分配
labels = assign_labels(X, centroids);
% 更新簇质心
centroids = update_centroids(X, labels, K);
end
% 绘制聚类结果
colors = ['r', 'g', 'b'];
figure;
hold on;
for i = 1:K
plot(X(labels == i, 1), X(labels == i, 2), [colors(i) '*']);
plot(centroids(i, 1), centroids(i, 2), [colors(i) 'o'], 'MarkerSize', 10, 'LineWidth', 3);
end
title('K-means++ ');
legend('类别1', '质心1', '类别 2', '质心 2', '类别 3', '质心 3');
hold off;
% 初始化簇质心函数
function centroids = init_centroids(X, K)
% 随机选择一个数据点作为第一个质心
centroids = X(randperm(size(X, 1), 1), :);
% 选择剩余的质心
for i = 2:K
D = pdist2(X, centroids, 'squaredeuclidean');
D = min(D, [], 2);
D = D / sum(D);
centroids(i, :) = X(find(rand < cumsum(D), 1), :);
end
end
% 簇分配函数
function labels = assign_labels(X, centroids)
[~, labels] = min(pdist2(X, centroids, 'squaredeuclidean'), [], 2);
end
% 更新簇质心函数
function centroids = update_centroids(X, labels, K)
centroids = zeros(K, size(X, 2));
for i = 1:K
centroids(i, :) = mean(X(labels == i, :), 1);
end
end
K-means聚类优化的算法中还有著名的K-medoids聚类,其原理和实现效果也很佳。


